آزمون جامع شماره 15

این مطلب توسط نویسنده‌اش رمزگذاری شده است و برای مشاهده‌ی آن احتیاج به وارد کردن رمز عبور دارید.

حال دوستتون خوبه

به لطف خدا به خیر گذشت . 

همانطور که می دانید حادثه  ای برای دوستمون برومند پیش اومد که به لطف پروردگار مهربان و دعای دوستان خوبش اتفاق خاصی نیفتاده و همین الان که حالش را از مادر محترمشان پرسیدم خوب است و جای نگرانی نیست . 

این دسته گل را از طرف خودم و همه ی دوستانش بهش تقدیم می کنیم 

از همه ی شما دوستان خوبم می خواهم برای دوست دیگرتون که امروز قراره عمل بشه دعا کنید که عملش به خوبی پیش بره و سلامتیش را دوباره به دست بیاره . 

کتاب شیمی ( اسید ها و باز ها )

این مطلب توسط نویسنده‌اش رمزگذاری شده است و برای مشاهده‌ی آن احتیاج به وارد کردن رمز عبور دارید.

جزوه ورزش و نیرو و انرژی

این مطلب توسط نویسنده‌اش رمزگذاری شده است و برای مشاهده‌ی آن احتیاج به وارد کردن رمز عبور دارید.

چند معما برای سنین مختلف

ساخت اعداد با اعمال ریاضی   تعدادی عدد را با شرایط داده شده بسازید.

معمای ریاضی: ساخت اعداد با اعمال ریاضی

آیا می توانید اعداد زیر را با شرایطی که عنوان شده بسازید؟ (می توانید از 4 عمل اصلی استفاده نمایید.) عدد 23 را بسازید ←    فقط با استفاده از عدد 2 عدد 34 را بسازید ←    فقط با استفاده از عدد 3 عدد 56 را بسازید ←    فقط با استفاده از عدد 5 عدد 100 را بسازید ← فقط با استفاده از عدد 9   سطح معما: بسیار ساده

پاسخ معمای ریاضی 'ساخت اعداد با اعمال ریاضی' یک سری از جواب های ممکن را در زیر مشاهده می کنید: 22+2/2=23 33+3/3=34 55+5/5=56 99+9/9=100

---

اثبات کنید. 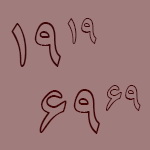توانایی های خود را در اثبات مسائل ریاضی محک بزنید.

مسأله ریاضی: اثبات کنید.

ثابت کنید عدد 6969+1919 بر 44 قابل قسمت است.           [سعی کنید قبل از مراجعه به جواب، حتما برای اثبات آن تلاش کنید...]

پاسخ مسأله ریاضی 'اثبات کنید.' راه حل اول: ثابت می کنیم عدد s=1919+6969 بر 4 و 11 قابل قسمت است: S=(20-1)19+(68+1)69 = (20m-1)+(68n+1)=4(5m+17n); S=(22-3)19 + (66+3)69 = 22m1+66n1+369-319 = 11p+319(350-1)= 11p+319(24310-1)=11p+319.242q=11q1 و چون S هم بر 4 و هم بر 11 قابل قسمت است، بر 44 نیز قابل قسمت است.

---

'تبدیل دوری ارقام' برای المپیادی ها و البته همه علاقمندان ریاضی :-)

معمای المپیادی: تبدیل دوری ارقام

عدد پنج رقمی مقابل را در نطر بگیرید: abcde این عدد بر 41 بخش پذیر است. ثابت کنید هر عددی که از تبدیل دوری رقم های این عدد به دست آید، بر 41 بخش پذیر است.

پاسخ معمای المپیادی 'تبدیل دوری ارقام' داریم:  bcdea = 10 abcde + a - 100000a = 10 abcde - 99999a و 99999 بر 41 بخش پذیر است، پس bcdea هم بر 41 بخش پذیر خواهد بود. به همین ترتیب ثابت می شود عددی که از تبدیل دوری عدد اخیر به دست می آید، یعنی cdeab هم بر 41 بخش پذیر است و به همبن ترتیب برای بقیه.

---

 

ضرب اختصاصی و مشارکت ارقام برای دوستداران محاسبه، علی الخصوص ضرب کردن!

معمای ریاضی: ضرب اختصاصی و مشارکت ارقام

ضرب زیر را در نظر بگیرید    *** ×   3*  -------  **** آیا می توانید بجای ستاره ها، ارقام 1 تا 9 (البته بجز 3 که جایش مشخص شده) را طوری قرار دهید که حاصلضرب درست باشد؟        [قبل از مراجعه به جواب معما، حتما کمی فکر کنید....]

پاسخ معمای ریاضی 'ضرب اختصاصی و مشارکت ارقام' پاسخ معمای ریاضی 'ضرب اختصاصی و مشارکت ارقام' پاسخ ما به این معما:    186 ×   39  -------   7254 آیا شما حاصلضرب دیگری بدست آورده اید؟ اگر چنین است آنرا منتشر نمایید.

---

معمای المپیادی: عدد 20 رقمی

دو دوست برای ساختن یک عدد 20 رقمی با شرایطی خاص، مسابقه می دهند...

معمای المپیادی: عدد 20 رقمی

کولیا و جسیکا، دو دوست هستند و با هم قراری می گذارند: تنها به کمک رقم های 1، 2، 3، 4 و 5، یک عدد 20 رقمی را می نویسند. رقم اول (از سمت چپ) را کولیا، رقم دوم را جسیکا می نویسد و به همین ترتیب. جسیکا می خواهد ترتیبی بدهد که عدد 20 رقمی حاصل، بر 9 بخش پذیر باشد. آیا کولیا می تواند مانع او بشود؟

پاسخ معمای المپیادی 'عدد 20 رقمی' بله می تواند. کولیا در گام اول رقم 1 را می نویسد و از آن به بعد، به دنبال رقمی که جسیکا می نویسد، کولیا رقمی می گذارد که با رقم اول جسیکا، روی هم برابر 6 شود. در این صورت مجموع 19 رقم اول، برابر 55 می شود. برای اینکه این عدد 20 رقمی بر 9 بخش پذیر باشد، باید رقم آخر برابر 8 باشد که چنین رقمی در اختیار جسیکا نیست.

---

معمای کسری با همان ارقام کسری را با شرایط مسئله بیابید...

معمای ریاضی: کسری با همه ارقام!

آیا می توانید ارقام 1 تا 9 را طوری در یک کسر استفاده کنید (هر رقم را فقط و فقط یک بار) که کسر حاصل، معادل 1/3 شود؟                                                                  مثال: (که البته مساوی 1/3 نیست!)       [سعی کنید بدون فکر کردن به جواب معما مراجعه نکنید...]

پاسخ معمای ریاضی 'کسری با همه ارقام!' پاسخ معمای ریاضی 'کسری با همه ارقام!' دو مورد از جواب های ممکن: (به شباهت بسیار زیاد دو جواب با یکدیگر دقت کنید...)

---

مدرسه مشترک می خواهیم بین دو روستا، مدرسه مشترکی بسازیم...

معمای ریاضی: مدرسه مشترک!

فاصله بین دو دهکده A و B از هم برابر 3 کیلومتر است. 100 دانش آموز در دهکده A و 50 دانش آموز در دهکده B زندگی می کنند. در چه فاصله ای از دهکده A یک مدرسه ساخته شود تا مجموع راهی که 150 دانش آموز روی هم می پیمایند، کمترین مقدار ممکن باشد؟

پاسخ معمای ریاضی 'مدرسه مشترک!' مدرسه باید در روستای A ساخته شود.

---

احداث راه یک شرکت راه سازی، ساختن جاده ای را به عهده می گیرد...

معمای المپیادی: احداث راه

یک شرکت راه سازی، ساختن جاده ای به طول 100 کیلومتر را به عهده می گیرد. برنامه ای که شرکت برای احداث این جاده ارائه نموده است به شرح زیر است:   -- در ماه اول یک کیلومتر از آن آماده خواهد شد. -- پس از آن، هر ماه 1/a10   (یک تقسیم بر a10) کیلومتر از جاده آماده خواهد شد که در آن a اندازه ساخته شده ی جاده تا ابتدای آن ماه است (بر حسب کیلومتر)   به نظر شما آیا وافعا این جاده آماده بهره برداری خواهد شد؟!

پاسخ معمای المپیادی 'احداث راه' بعد از یک ماه، همیشه بخشی از جاده که آماده نشده است، از 100 کیلومتر کمتر است. بنابراین هر ماه دست کم 1/10010 کیلومتر از جاده ساخته می شود و به این ترتیب بعد از 10011 ماه، جاده آماده بهره برداری می شود!

---

محاسبه تعداد صفرها محاسبه تعداد صفرهای عدد داده شده!

مسأله ریاضی:محاسبه تعداد صفرها

اگر عدد !10 (که عدد 10 در پایه 10 نوشته شده است) در پایه 12 نوشته شود، دقیقا به چند صفر ختم می شود؟                                                                                                                                 [قبل از مراجعه سریع به جواب مسئله، برای حل آن تلاش کنید...]

پاسخ مسأله ریاضی 'محاسبه تعداد صفرها' 4 صفر   در پایه 10 داریم: 10! = 1×2×3×4×5×6×7×8×9×10 = 28×34×52×7 = 124×52×7 52×7=175 = 1×122 + 2×12+7 [52×7×124]10= [127×104]12 = [1270000]12 همانطور که می بینید این عدد دقیقا به 4 تا صفر ختم می شود.

---

حاصلضرب مینیمم! می خواهیم سه عدد با شرایط خاصی بسازیم....

معمای ریاضی: حاصلضرب مینیمم!

اعداد 1 تا 9 را در نظر بگیرید. می خواهیم با این ارقام، 3 عدد 3 رقمی بسازیم (از هر رقم تنها می توانیم تنها یک بار استفاده کنیم) که حاصلضرب آنها مینیمم (کمینه) باشد. آیا می توانید این سه عدد را بیابید؟

پاسخ معمای ریاضی 'حاصلضرب مینیمم!' اعداد زیر عبارتند از:  147، 258 و 369.   حاصلضرب این اعداد برابر است با: 13,994,694   می توانید با ماشین حساب کمی  اعداد مختلف را امتحان کنید، فقط به یاد داشته باشید اعداد انتخابی شما با 1، 2 و 3 شروع شوند...

---

معمای المپیادی: مجموع ارقام مجذور A عددی داریم، می خواهیم مجموع ارقام مجذورش را محاسبه کنیم...

معمای المپیادی: مجموع ارقام مجذور A

عدد A را بصورت زیر در نظر بگیرید:    A=            81 بار          مجموع ارقام  A2 در پایه 10 چند است؟    الف) 693    ب) 729    ج) 790    د) 837    هـ) 936

پاسخ معمای المپیادی 'مجموع ارقام مجذور A' گزینه ب صحیح است.   توجه کنید که  1 - 1081 = A بنابراین: A2=10162 - 2  1081 + 1 پس نمایش دهدهی A2 به صورت زیر خواهد بود:   80 بار                پس مجموع رقمهای A2 در پایه 10 برابر است با: 9  80 + 8 + 1 = 729

---

عدد اول همسایه عدد مکعب! عددی بیابید که اول باشد و شرایط این مسئله را داشته باشد...

معمای ریاضی: عدد اول همسایه عدد مکعب!

عدد 7 یک عدد اول است که دقیقا قبل از یک عدد مکعب کامل (23=8) قرار دارد. آیا می توانید عدد اول دیگری با این خصوصیت بیابید؟

پاسخ معمای ریاضی 'عدد اول همسایه عدد مکعب!' خیر، عدد اول دیگری با چنین مشخصه ای وجود نخواهد داشت. در واقع عدد 7، تنها عدد اولی است که دقیقاً قبل از یک عدد مکعب کامل قرار گرفته است.   فرض کنید n3-1 به ازاء برخی از nها، اول باشد. داریم: n3-1 = (n−1)(n2+n+1) بنابراین n3-1 بر n-1 بخشپذیر خواهد بود و به ازاء  n-1>1، عدد n3-1 دیگر نمی تواند اول باشد!

---

معمای طوطی در قفس تعدادی طوطی و تعدادی قفس در اختیار داریم...

معمای ریاضی: طوطی های در قفس!

تینا تعدادی طوطی و تعدادی قفس در اختیار دارد. اگر او در هر قفس 4 طوطی قرار دهد، یک قفس، خالی باقی می ماند. اگر او در هر قفس 3 طوطی قرار دهد، یک طوطی بدون قفس خواهد ماند. آیا می توانید بگویید تینا چند طوطی و چند قفس دارد؟     [با کمی فکر و دقت در صورت معما، به جواب خواهید رسید...]

پاسخ معمای ریاضی 'طوطی های در قفس!' با توجه به صورت معما داریم:  بخش نخست: تعداد طوطی ها برابر است با 4 برابر تعداد قفس ها منهای یک: 1)   P = 4(C - 1) بخش دوم: تعداد طوطی ها برابر است با سه برابر تعداد قفس ها به علاوه یک: 2)   P = 3C + 1 با حل این دو معادله، خواهیم داشت:  تعداد طوطی ها: 16

---

معمای ریاضی: معمای سال 2013! با بررسی ارقام سال 2013 میلادی، سوالاتی مطرح می شود...

معمای ریاضی: معمای سال 2013!

با بررسی ارقام سال گذشته میلادی، سال 2013، سه سوال مطرح می کنیم:    الف. با بررسی ارقام این سال (2013)، می بینیم که شامل چهار رقم متفاوت بوده است. آیا می توانید بگویید آخرین بار قبل از این سال، چه سالی این خصوصیت را دارا بوده است؟   ب. ارقام سال 2013 شامل 4 رقم پشت سر هم از 0 تا 3 بوده است. آخرین بار قبل از آن چه تاریخ مشابهی وجود داشته است؟ (لزوما نباید این 4 رقم، ارقام 0، 1، 2، 3 باشند!)   ج. ارقام سال 2013 شامل 4 رقم پشت سر هم از 0 تا 3 بوده است. نزدیک ترین تاریخی که در آینده چنین باشد، چه سالی خواهد بود؟ (لزوما نباید این 4 رقم، ارقام 0، 1، 2، 3 باشند!)

پاسخ معمای ریاضی 'معمای سال 2013!' الف. 1987   ب. 1432   ج. 2031

---

خرید و فروش گوسفندان   کشاورزی مبادرت به خرید و فروش تعدادی گوسفند می نماید...

مسأله ریاضی: خرید و فروش گوسفندان

کشاورزی 749 گوسفند می خرد. 700 گوسفند را روی هم به مبلغی معادل با مبلغ خرید 749 گوسفند می فروشد. هر رأس از 49 گوسفند باقیمانده را به قیمت یک رأس از 700 گوسفند فروخته شده قیمت گذاری می کند و آن ها را می فروشد. او در کل این معامله چند درصد سود می کند؟

پاسخ مسأله ریاضی 'خرید و فروش گوسفندان' مبلغ خرید 749 گوسفند را P می گیریم. قیمت فروش هر رأس گوسفند، P/700 و کل سود 49xP/700 است. بنابراین سود کشاورز چنین است: (49 x P/700)/P x 100 = 7

---

انجام کار

سه ماشین R، Q، P کاری را با هم در زمان مشخصی انجام می دهند...

مسأله ریاضی: انجام کار

سه ماشین R، Q، P کاری را با هم در x ساعت انجام می دهند. همان کار را P به تنهایی با 6 ساعت اضافه، Q به تنهایی با یک ساعت اضافه، R به تنهایی با x ساعت اضافه انجام می دهند. مقدار x برابر است با:   الف) 2/3  ب) 11/12   ج) 3/2   د) 2  هـ) 3

پاسخ مسأله ریاضی 'انجام کار' پاسخ مسأله ریاضی 'انجام کار' الف)     1 / x  نشاندهنده بخشی از کار است که هر سه ماشین با هم در 1 ساعت انجام می دهند، و به همین ترتیب برای سه حالت دیگر، پس:   یا بصورت ساده تر:   بنابرین: 2x(x+1)+2x(x+6)-(x+6)(x+1)=0 یا 3x2+7x-6=0

---

معادله منطق!

9" 3="" 5="" 7="" 8="" dir="ltr" href="http://ihoosh.ir/Articles/Article.aspx?id=61381" id="ctl00_ContentPlaceHolder1_rptArticle_ctl09_A1" span="" title="9 برای هر قسمت، یکی از جواب های ممکن ارائه شده است: 1. 57 = 78125   2. (1+9+6+8+3)3 = 19683

---

5 تا 5 تا بشمرم چهار تا زیاد می آید" " اگر آنها را 4 تا 4 تا بشمرم سه تا زیاد می آید" " اگر آنها را 3 تا 3 تا بشمرم دو تا زیاد می آید" " اگر آنها را 2 تا 2 تا بشمرم یکی زیاد می آید" تعداد گوسفندان این چوپان چند راس بوده است؟   معمای هوش یافتن عدد گمشده اگر اعدادی مطابق زیر داشته باشیم با یافتن رابطه میان آنها عدد گمشده را پیدا کنید. 382      13      661 429      15      780 551      11      821 158      14      716 933       ?       258 یه معمای جادویی اعداد 2 و 3 و 4 و 5 را طوری داخل دایره ها قرار دهید که در هر هشت ردیف، مجموع اعداد 14 شود . توجه کنید که هر عدد در هر ردیف فقط یکبار تکرار می شود... معمای صفحه شطرنج نامتناهی صفحه شطرنجی رو در نظر بگیرید که از طرف راست و بالا نامتناهی است ... می خواهیم تمام اعداد طبیعی رو در هر سطر و هر ستون بنویسیم به طوری که در هر سطر تمام اعداد طبیعی را داشته باشیم و در هر ستون هم همین طور ... اعداد در هر سطر و هر ستون نباید تکراری بیایند. معمای حداقل تعداد تخم مرغهای زن روستائی  یک زن روستائی یک سبد تخم مرغ به میدان می برد که بفروشد. هنوز هیچ نفروخته بود که پای اسب یک سوار به سبد تخم مرغ زن خورد و بیشتر تخم مرغ ها شکست. اسب سوار از زن روستائی پوزش خواست و حاضر شد پول همه آنها را بپردازد. اسب سوار: مادر جان چند تا تخم مرغ داشتی؟ زن روستائی: نمی دانم ! ، اما وقتی آنها را دوتا دوتا بر میداشتم یکی باقی می ماند ، وقتی سه تا سه تا بر میداشتم یکی باقی می ماند ، وقتی چهارتا چهارتا بر میداشتم یکی باقی می ماند ، وقتی پنج تا پنج تا بر میداشتم یکی باقی می ماند ، وقتی شش تا شش تا بر میداشتم یکی باقی می ماند ، اما وقتیکه هفت تا هفت تا بر میداشتم هیچی باقی نمی ماند. اسب سوار حساب کرد و پول تخم مرغ های زن روستائی را داد. سوال: کمترین تعداد تخم مرغی که زن روستائی میتوانست در سبد داشته باشد چند تا بود؟ معمای دنباله ریاضی ! جای خالی رو با یه عدد مناسب پر کنید: ...-91-48-25-12-6-2-1    معمای یک دلاری     سه نفر در هتلی یک اتاق می گیرند ، هتلدار بابت یک شب کرایه اتاق 75 دلار از آنها می گیرد ، ولی بعدا متوجه می شود که اشتباه کرده است و بایست 70 دلار می گرفته است. او 5 دلار به پیشخدمت هتل می دهد که برای مسافران ببرد. پیشخدمت فکر می کند که سه نفر نمیتوانند 5 دلار را به طور مساوی بین خود تقسیم کنند. پس تصمیم می گیرد 3 دلار به آنها بدهد و 2 دلار را برای خودش بردارد ...  بعدا پیشخدمت با خود فکر می کند که هر یک از مسافران 24 دلار (یعنی 25 دلار منهای 1 دلار ) برای کرایه اتاق پرداخت کرده اند و خودش هم2 دلار دارد ... این می شود 74 دلار  74=2+24×3 یک دلار دیگر چه شده است؟ معمای تقسیم سکه 5 دزد دریایی با سن های مختلف، صندوقی شامل 100 سکه طلا به دست می آورند و قصد تقسیم آنرا دارند.  روش تقسیم به این صورت است که مسن ترین آنها طرحی برای تقسیم ارائه می کند، سپس هر 5 نفر به این طرح رای می دهند. اگر 50% یا بیشتر رای مثبت به دست آید طرح اجرا می شود وگرنه شخص ارائه کننده ی طرح را به دریا می اندازند. و این کار با نفر بعدی که مسنتر است تکرار میشود. چون این دزدان سعی می کنند رقیب را حذف کنند، پس اگر رای مثبت یا منفی هر یک از آنها تاثیری در سهمش نداشته باشد حتما رای منفی می دهید. با توجه به اینکه هرکدام می خواهند بیشترین سهم را داشته باشند و نمی خواهند به دریا انداخته شوند، در پایان سکه ها به چه روشی تقسیم میشوند؟ یه معمای احتمالاتی سی نفر به تصادف در اتاقی جمع شده اند. احتمال این که تاریخ تولد(ماه وروز) دونفر از آنها یکی باشد چقدر است؟   معمای کارت ها سه بازیکن A,B,C دور یک میز نشسته اند و دارند بازی زیر را انجام میدهند سه کارت روی میز گذاشته شده است.  روی هر کدام از این کارت ها سه عدی نوشته شده است که با 2 کارت دیگر فرق دارد لم بازی: "در هر دور از بازی هر نفر کارتی را بر می دارد و به اندازه ی عددی که روی آن کارت است مهره دریافت می کند." در ضمن جزو قوانین بازی است که بازیکن ها لااقل 2 دور لم را اجرا کنند. پس از چند دور بازی کردن حوصله این سه نفر از این بازی مهیج(!) سر می رود و تصمیم به شمارش مهره ها می کنند. اگر به شما بگویند نفر A در پایان بازی 20 مهره و نفرB هم10 مهره و C هم 9 مهره جمع کرده و این نکته را هم بدانید در آخرین باری که لم اجرا شده B کارتی را برداشته که عدد آن از همه بزرگتر است مشخص کنید روی هر کدام از سه کارت چه عددی نوشته شده و این که در هر دور هر کس چه امتیازی گرفته است.   معمای عدد صحیح کوچکترین عدد صحیح را بیابید که دارای جذر کامل یاشد و با ۱۹۸۹ شروع شود! معما روی خط                 دو قطار زیر زمینی یکی دو برابر سریعتر از دیگری از دو سر یک خط به راه  افتادند و بدون توقف با سرعت یکنواخت حرکت کردند و در خیابان پنجاهم از کنار هم رد شدند. اگر قطار سریعتر در اغاز حرکت 5 دقیقه تاخیر داشت در نقطه ای به فاصله 2 کیلومتر از خیابان پنجاهم به هم میرسیدند.به نظر شما سرعت قطار ها چقدر است ؟ طول خط چه اندازه است؟ معمای زمان                  مدت زمانی که دو ساعت دیگر تا نیمه شب باقی است نصف مدت زمانی است که یک ساعت دیگر تا نیمه شب زمان داریم. هم اکنون ساعت چند است؟ معمای تاس ها                  اگر دو تاس را همزمان با هم پرتاب کنید احتمال این‌که مجموع اعداد ظاهر شده عددی فرد باشد چقدر است؟   معمای حبه قندها                     10 تا جعبه قند داریم.  هر جعبه از 1000 حبه قند تشکیل شده.  وزن هر حبه قند 10 گرمه.  این وضعیت تو همه جعبه ها همین طوریه ولی فقط یکی از جعبه ها حبه هایی با وزن 9 گرم داره.  یه ترازو داریم که یه بار مصرفه. یعنی فقط میشه یه بار با اون وزن کرد و بعد از اون دیگه از کار می افته.  می خوایم با استفاده از این ترازو و تنها با یک بار وزن بفهمیم کدوم جعبه وزن کمتری داره.  چطور این کار رو انجام دهیم؟؟ معمای جالب ساعت شنی              دوتا ساعت شنی داریم یکی 3 دقیقه را محاسبه میکند و یکی 7 دقیقه را ما میخواهیم 8 دقیقه را حساب کنیم.  توجه کنید ما مستقیم زمان 8 دقیقه را میخواهیم نه اینکه بشینین 1 ساعت جمع و کم کنید تا 8 دقیقه بشه .یعنی از وقتی که هر کدام از این ساعت شنی ها را فعال کردین زمان 8 دقیقه شما شروع میشود و باید 8 دقیقه را محاسبه کنید.   معمای چینش اعداد در دایره ها                       در هر یک از قسمت‌های رنگی‌شکل، عددی از یک تا 6 قرار دهید به گونه‌ای که اعدادی که در قسمت‌های همرنگ و همچنین اعدادی که در یک دایره قرار می‌گیرد، تکراری نباشد.    معمای جدول اعداد                             به جدول اعداد زیر دقت کنید.در آخرین خانه به جای ؟ چه عددی باید جایگزین شود.   195 383 575 763 955 ؟ معمای رابطه اعداد                     در شکل زیر دقت کنید و با توجه به رابطه بین اعداد مشخص کنید چه عددی باید به جای علامت سئوال قرار گیرد؟   معمای سربازان                       در یک جنگ ۱۰۰ سرباز شرکت کردند و جراحاتی برداشتند. آمار جراحات به شرح زیراست: ۷۰ نفر دست راستشان را از دست دادند ۷۵ نفر دست چپشان را از دست دادند ۸۰ نفر پای راست ۸۵ نفر پای چپ از دست دادند. حد اقل تعداد افرادی که هر ۴ عضوشان را از دست دادن چندتاست؟   معمای برابری جمع و ضرب   شش عدد صحیح مثبت چنان بیابید که مجموعشان با حاصل ضربشان برابر باشند. معمای طول نردبان                   نردبانی داریم که اگر کنار دیوار، بطور قائم قرار گیرد نوک نردبان از انتهای دیوار ۱۰ سانتیمتر بالاتر قرار می گیرد. و هرگاه پای همین نردبان را از پای همان دیوار ۷۰ سانتیمتر فاصله بدهیم نوک نردبان به انتهای دیوار منطبق می شود. طول نردبان را پیدا کنید.    سرگرمی به توان رساندن اعدادی که یکان آنها به یک ختم می شود     نکته ای که باید بدانید اینکه:   (21)2 - (20)2=21+20    با دونستن این نکته دیگه کار تمام است.   مرحله1:یک عدد پایین تر را به توان دو می رسانیم   مرحله2:خود عدد را با با یک عدد از خود پایین تر را جمع می کنیم   مرحله3:دو عدد بدست آمده از مرحله های قبل را با هم جمع می کنیم   مرحله4:جواب بدست آمده.                      مرحله4           مرحل3         مرحله 2            مرحله 1   (41)2=          (40)2               41+40          1600+81            1681   (71)2=          (70)2               71+70          4900+141           5041   توجه کنید که به توان رساندن اعدادی که رقم یکان آنها 6 است، به روش مشابهی انجام می شود. کمی دقت کنید خودتان می توانید مراحل را انجام دهید. سرگرمی تقسیم سریع اعداد بر عدد هایی که به صورت1.5 ، 2.5 ، 3.5 ، 4.5 ، ...   مرحله1:عدد  را  در عدد 2 ضرب می کنیم.   مرحله2:عدد1.5 ، 2.5 ، 3.5 ، 4.5 ، ... را در 2 ضرب می کنیم.   مرحله3:اعداد بدست آمده را برهم تقسیم می کنیم.   مرحله4:جواب بدست آمده.                        مرحله4           مرحله3           مرحله 2           مرحله 1   30 ÷ 1.5=        30 × 2            1.5 × 2             60÷3               20   90÷4.5=         90× 2             4.5 × 2             180÷9              20   26÷6.5=         26× 2             6.5× 2             52÷13               4 چرا ۱۴ مارس روز عد پی نامگذاری شده است؟                                               این نامگذاری به علت سه رقم اول عدد پی ( یعنی ۳.۱۴)میباشد.یعنی روز چهاردهم از سومین ماه میلادی،البته بد نیست بدانیم آلبرت انیشتین هم در این روز چشم به جهان گشود.   اعداد صلح آمیز به زوجی از اعداد که حاصل جمع شمارنده های یکی با دیگری برابر باشد و بالعکس اعداد صلح آمیز می¬گویند. اولین زوج صلح آمیز۲۲۰و۲۸۴هستند که به این شکل اند .مقسوم¬علیه های۲۸۴ عبارت است از ۱و۲و۴و۷۱و۱۴۱ وحاصل جمع شمارنده های آن برابر ۲۲۰.                                                                           حالا مقسوم علیه های ۲۲۰ عبارت است از۱و۲و۴و۵و۱۰و۱۱و۲۰و۲۲و۴۴و۵۵و۱۱۰ وحاصل جمع مقسوم علیه هایش برابر 284 . دومین زوج صلح آمیز کشف شده۱۱۸۴و۱۲۱۰هستند که به این شکل اند . مقسوم علیه های ۱۱۸۴عبارت است از ۱و۲و۴و۸و۱۶و۳۲و۳۷و۷۴و۱۴۸و۲۹۶و۵۹۲ ، و حاصل جمع مقسوم علیه هایش برابر۱۲۱۰. مقسوم علیه های ۱۲۱۰ عبارت است از ۱و۲و۵و۱۰و۱۱و۲۲و۵۵و۱۱۰و۱۲۱و۲۴۲و۶۰۵ ،  و حاصلجمع مقسوم علیه ها برابر ۱۱۸ . محاسبه جذر اعداد با فرجه دلخواه     با استفاده از این روش می توانید جذر اعداد را با فرجه دلخواه محاسبه نمایید . این روش دارای حد اکثر پنج صدم خطا می باشد و روش مناسبی برای جذر گیری است. با استفاده از فرمول زیر می تواند حاصل جذر را به صورت یک کسر به دست آورده و در صورت تمایل با تقسیم صورت بر مخرج حاصل را به طور تقریبی بیابید. فرمول کلی به شکل زیر است. مثال: حاصل جذر را های زیر را بیابید. توجه کنید که هر چه عدد مورد نظر بزرگ تر باشد خطای جذر گیری با استفاده ز این روش کمتر می باشد .معمای احتمالاتی بیمارها   فرض کنید با دو بیماری مواجهیم؛ Aو  B که نشانه های مشاهده پذیر شان عمیقا عین هم اند. %90 کسانی که این نشانه ها را دارند به بیماری A مبتلایند؛ %100 دیگر بیماری B را دارند. همچنین فرض کنید آزمایش آسیب شناختی ای داریم که A وB را از هم تشخیص می دهد. آزمایش از 10بار 9 بار جواب صحیح می دهد. 1. احتمال این که آزمایش بیماری B را اعلام کند چه قدر است وقتی افرادی که نشانه های بیماری را دارند کاملاً به طور تصادفی انتخاب شده باشند؟( نکته: 100 نفر را انتخاب کنید و مشخص کنید که با چند بار آزمایش بیماری B برایشان تشخیص داده می شود ). 2. احتمال این که کسی با همان نشانه های مذکور به بیماری B مبتلاً باشد چه قدر است، به شرط این که آزمایش بگوید آن شخص به بیماری B مبتلا است؟ ( نکته: باید از سؤال اول استفاده کنید ). معمای الگوی اعداد آیا میتوانید سطر بعدی را حدس بزنید؟؟؟؟؟؟؟؟ 1 1 1 2  1 1 2 1 1 1 1 1 2 2 1 3 1 2 2 1 1 1 3 1 1 2 2 2 1 1 1 1 3 2 1 3 2 1 1 3 1 1 3 1 2 1 1 1 3 1 2 2 1 ......................................................?   اگر کمی با انگلیسی آشنایی دارید به صفحه زیر بروید: صفــــحـــــــــــــــــه ببینید آیا فکر شما را هم می خواند؟ سن آقای میوه فروش وتعداد بچه هایش معلم ریاضی: آقای میوه فروش چند تا بچه داری؟ و چند ساله هستند؟ میوه فروش: 3 تا بچه دارم که حاصل ضرب سن آنها 72 و مجموع سن آنها 14 می باشد. معلم ریاضی: من سن بچه های شما را یافتم ولی یک راهنمایی نیاز دارم. میوه فروش: راهنمایی اینکه فرزند بزرگترم به بازی های کامپیوتری علاقه ای ندارد. معلم ریاضی: اکنون سن دقیق فرزندان شما را می دانم. سکه ی تقلبی    12 سکه داریم که یکی از آنها تقلبی است(معلوم نیست سنگین تر از بقیه است یا سبکتر) می خواهیم با سه بار وزن کردن  سکه تقلبی را پیدا کنیم. غیب گویی با ریاضیات روی میزی پنج جسم قرار دهید , طوریکه تعداد حروف تشکیل دهنده اسم اجسام از 9 بیشتر نباشد و اجسام از نظر تعداد حروف یکسان هم نباشند. مانند کاغذ که چهار حرفی است و خودنویس که هفت حرفی است. سپس از حاضرین تقاضا کنید که دور از چشم شما پنج جسم در کاغذی لیست کنند بطوریکه تعداد حروفشان برابر نباشد. سپس بصورتی که شما دستور می دهید عمل نمایند. نحوه عمل اسم یکی از پنج جسم را به دلخواه در ذهن خود انتخاب نمایند.   تعداد حروف آنرا در عدد 5 ضرب کنند.   به این حاصلضرب عدد 3 را اضافه کنند.   حاصل جمع به دست آمده را در عدد 2 ضرب کنند.   به حاصل ضرب بدست آمده رقم دلخواهی (از 1 تا 9) اضافه نمایند.   نتیجه را به شما بگویند، تا شما بطور غیبی بگویید که آنها کدام جسم را انتخاب کرده‌اند و چه رقم دلخواهی رویش اضافه نموده اند.عدد نهایی گزارش شده به شما که بدون شک دو رقمی می‌باشد . از این عدد بطور ذهنی عدد 6 را کم کنید. پیش گویی غیبی رقم دهگان این عدد تعداد حروف جسم مفروض و در نتیجه خود جسم را مشخص می‌کند . رقم یکان این عدد , عدد دلخواه اضافه شده به این محاسبات را معین می‌کند . در این کار علاوه از ریاضیات پیش گویی غیبی و شعبده بازی نیز یاد گرفته‌اید. تعداد برادران وخواهران-شعبده ی ریاضی با کمی دقت می توانید تعداد دختران وپسران یک خانواده را حدس بزنید! 1- از یک نفر بخواهید که تعداد برادرانش را به اضافه 3 کند . 2- حاصل بدست آمده را در عدد 5 ضرب و عدد 20 را به آن اضافه کند . 3- حاصل به دست آمده را در عدد 2 ضرب و به تعداد خواهرها اضافه کند . 4- به حاصل، عدد 5 را اضافه و عدد 75 را از آن کم کند . 5- نتیجه را به شما بگوید . - عدد حاصل ( که دو رقمی است )، تعداد خواهران و برادران را مشخص می نماید. -عدد سمت راست تعداد خواهرها و عدد سمت چپ تعداد برادرها است.       در دنباله زیر عدد بعدی چند است؟ ... , 55 , 19 , 7 , 3 الف) 173       ب) 143          ج)153             د)163   ۱۳۸۳۷ را در سن خود ضرب کنید  و سپس حاصل را در 73  ضرب کنید. چه چیزی مشاهده کردید. آیا می توانید با توجه به آن چه از نظریه اعداد آموخته اید دلیل این امر را توضیح دهید؟ به جای علامت سوال چه عددی قرار دهیم؟   12  15  4  3  2  20  28  5  4  3 30  45  6  5  4 42  66  7  6  5 56  ؟    8  7  6  جواب معما برابر عدد زیر است. 7*(6+7)=  91 شخصی یک زنجیر دارد که دارای 7 حلقه است. می خواهد به مدت 7 شب در یک هتل بماند ، اما پولی برای پرداخت ندارد.صاحب هتل از زنجیر این شخص خوشش می آید ولذا پیشنهاد می کند که اگر بتواند فقط یک برش در زنجیر ایجاد کند که با آن یک برش هر شب یک حلقه زنجیر را به عنوان کرایه بردارد ، حاضر است قبول کند که آن شخص در هتل بماند. سوال این است که کدام حلقه را ببرد تا این کار را انجام دهد؟ اگر خواستید جواب را در ادامه ببینید. باید حلقه سوم (یا فرقی نمی کندچهارم) را ببرد. اگر حلقه سوم را ببرد زنجیر به سه قسمت تقسیم می شود. دو حلقه ای و یک حلقه ای و چهار حلقه ای. شب اول حلقه سوم را می پردازد. شب دوم یک حلقه را پس گرفته و دو حلقه ای را می پردازد. شب سوم تک حلقه ای را پرداخت می کند.شب چهارم سه حلقه داده شده را می گیرد و بعد قسمت چهار حلقه ای را می پردازد.در شب پنجم تک حلقه ای را و در شب ششم تک حلقه ای را گرفته و قسمت دو حلقه ای را می دهد و در شب آخر هم تک حلقه ی باقیمانده را پرداخت می کند.   محاسبه تعداد صفرهای 15 فاکتوریل مسأله ریاضی: 15 فاکتوریل اگر عدد !15 (1×2×3×4×5×6×7×8×9×10×11×12×13×14×15) در عدد نویسی در پایه 12 به k صفر  و عدد نویسی در پایه 10 به h صفر ختم شود، k+h برابراست با:   الف) 5   ب) 6   ج) 7   د) 8  هـ) 9 پاسخ مسأله ریاضی '15 فاکتوریل' د) 15! = 103×(3×14×13×12×11×9×8×7×6×3×2×1) 15! = 125×(15×14×13×11×5×7×5)   k=5 h=3 k+h=8 معمای ریاضی: عبور از بیابان سوزان! مسافری می خواهد از یک بیابانی با پای پیاده عبور کند که 12 روز به طول خواهد انجامید. او باید برای حمل آب و آذوقه مورد نیاز سفر باید تعدادی باربر روزمزد استخدام کند. آیا می توانید کمترین تعداد باربران لازم را برای این سفر، مشخص کنید. توجه داشته باشید که لازم نیست باربران تمام راه را با مرد مسافر همراه باشند. و نکته دیگر اینکه هر نفر (مسافر و باربران) می توانند آب و آذوقه مورد نیاز 8 روز یک نفر را با خود حمل کنند.   پاسخ معمای ریاضی 'عبور از بیابان سوزان'  2 نفر باربر برای این سفر کافیست.   پس از 2 روز 6 جیره از 8 جیره روزانه اولین باربر مصرف شده است (برای سه نفر). این باربر می تواند با دوجیره باقیمانده برگردد.   مسافر ما 2 روز دیگر با بار دوم به سفر ادامه می دهد و در این دو روز، 4 جیره باربر دوم نیز مصرف شده است. این باربر می تواند با 4 جیره مانده، برگردد.   مسافر ما اکنون با 8 جیره روزانه خودش که دست نخورده باقی مانده، 8 روز دیگر ادامه می دهد و سفر 12 روزه خودش را به آنسوی بیابان، به آخر می رساند.

یک در خواست

یک در خواست 

از دانش آموزانی که به وبلاگ سر می زنند خواهشمند است اگر تلفن برومند را دارید در بخش نظرات بگذارند تا بتوانم حال اورا جویا شوم 

با تشکر از شما 

آزمون جامع شماره 15

این مطلب توسط نویسنده‌اش رمزگذاری شده است و برای مشاهده‌ی آن احتیاج به وارد کردن رمز عبور دارید.