انیمیشن های ریاضی ششم

انیمیشن های ریاضی ششم دبستان

برای دانلود انیمیشن های ارائه شده باید برنامه سیو فلش نصب نمایید

کارگاهی برای یادگیری مقایسه کسر اعشاری

تمرینی برای یادگیری صعودی و نزولی بودن اعشار

کارگاه ساخت اعداد اعشاری

تمرینی برای یادگیری اعداد اعشاری بر روی محور

تمرینی جالب برای یادگیری تقسیم کسر

تمرینی جذاب برای یادگیری تبدیل کسر به اعشار

تمرینی جذاب برای یادگیری مقدار معینی از کسر

تمرینی برای یادگیری کسر به عددمخلوط

تمرینی برای یادگیری مضرب ومضرب مشترک

یک بازی جذاب برای یادگیری مضرب اعداد

یک بازی برای یادگیری ضرب و تقسیم کسرها

کارگاهی برای گنجایش

تمرینی برای یادگیری کسر به همراه شکل

اندازه گیری

خط تقارن

بادکنک های مهاجم

عدد بسیار اول

ایا می دانید عدد بسیار اول به چه عددی می گویند؟

من هم برایم بسیار جالب بود و دوست داشتم شما هم بدونید.

عدد 373 همان عدد مورد نظر است .  

از هر طرف به آن نگاه کنی عدد اول است.  

اگر یک رقم یک رقم در نظر بگیریم ،هر رقمی یک عدد اول است.  

و همینطور اگر دو رقم د و رقم در نظر بگیریم

باز هم اعداد اول داریم. و خود عدد هم که سه رقمی است نیز عددی اول است. 

 پس به این عدد ،  

عدد بسیار اول می گوئیم .

جالب بود نه؟؟؟؟؟  

مساحت مثلث

می دانیم که مساحت مثلث در حالت کلی برابر است با 

  2 /  ( قاعده × ارتفاع ) = مساحت مثلث 

در این روش ، فرمولی ارائه می شود که شما را  قادر  می سازد مساحت هر نوع مثلثی را با دانستن مقدار 3 ضلع آن محاسبه کنید                  

فرض کنیم a و b و  c  سه ضلع مثلث را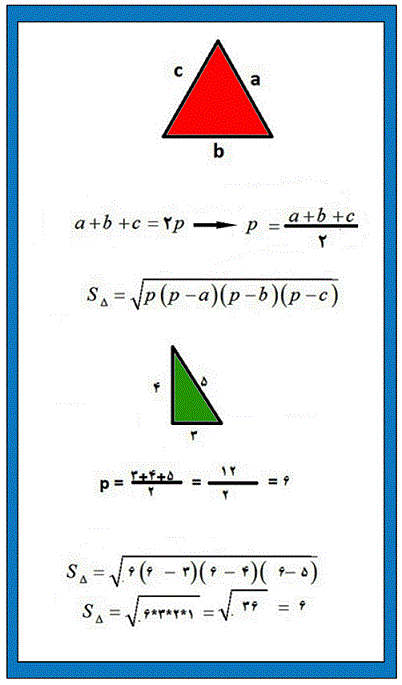   

چنر سوال جالب

 

 

نمونه آزمون های ریاضی

نمونه آزمون های ریاضی

  چهارم ابتدایی

پنجم ابتدایی

اول راهنمایی

دوم راهنمایی

سوم راهنمایی

روش حل مسئله به روش پویا نمایی

رسم چند ضلعی منتظم:

برای رسم یک n ضلعی منتظم کافی است دایره ای را به n قسمت مساوی تقسیم کرده و نقاط تقسیم را به هم وصل کنیم .

تقسیم دایره به n قسمت مساوی به صورت زیر انجام می شود:

1. یک زاویه ی مرکزی به اندازه ی رسم کنیم .

2.وتر نظیر این زاویه مرکزی را می کشیم .

3. پرگار را به اندازه ی این وتر باز کرده و پشت سر هم کمان های متوالی می زنیم تا دایره به n قسمت مساوی تقسیم شود .

مثال:

شش ضلعی منتظم:

زاویه ی ظلّی :

هر زاویه ای که رأسش روی دایره و یک ضلع آن وتری از دایره و ضلع دیگرش بر دایره مماس باشد ، زاویه ی ظّلی نامیده می شود.

در شکل مقابل یک زاویه ی ظّلی و کمان AB کمان مقابل به زاویه ی ظّلی A می باشد.

نکته : اندازه ی زاویه ی ظّلی نصف کمان مقابل آن است.

 وتر و یک زاویه تند (حاده):

اگر وتر یک زاویه تند (حاده) از مثلث قائم الزاویه ای با وتر یک زاویه ی تند (حاده) از مثلث قائم الزاویه دیگری مساوی باشند ، آن دو مثلث مساوی اند .

وتر و یک ضلع:

اگر وتر و یک ضلع مثلث قائم الزاویه ای با وتر و یک ضلع مثلث قائم الزاویه دیگری مساوی باشند ، آن دو مثلث قائم الزاویه با هم مساویند .

زهرا نقاشی مقابل را کشیده است  او می خواهد شلوار پسرک را سبز ، قرمز ، آبی  یا بنفش و پیراهن او را سبز ، زرد ، یا قرمز رنگ کند او به چند صورت می تواند این نقاشی را رنگ کند ؟

حل: 12=3×4            12 حالت 

برای رفتن از شهر A به شهر B سه راه وجود دارد . از شهر B به شهر C نیز 2 مسیر مختلف وجود دارد حساب کنید برای رفتن از شهر A به شهر C چند مسیر وجود دارد ؟

حل: 6=2×3

(sieve Algorithm of Eratosthenes)

اراتستن نام ریاضی دان و منجم یونانی است و غربال در فارسی به معنی جداکردن می باشد و الگوریتم به روشی از محاسبه گفته می شود که در آن ، محاسبات مرحله به مرحله انجام می شود و محاسبه هر مرحله نیز به مراحل قبلی بستگی دارد.

مراحل کار برای تعیین عددهای اول بین 1 و عدد طبیعی n به ترتیب نمودار زیر انجام می شود.

امتحان جذر:

اگر یک جذر را درست انجام داده باشیم:

الف_- دو برابر جذر به اضافه یک از باقیمانده ی جذر بزرگتر است.

ب_- مجذور جذر به اضافه باقیمانده ، مساوی عدد داده شده است.

نکته: اگر بخواهیم جذر یک عدد اعشاری را امتحان کنیم، در مورد قسمت الف قبل از درج ممیزها، امتحان جذر را انجام می دهیم.

معمای جالب ریاضی

معمای جالب ریاضی 

 

 ۱-

در یک جنگ ۱۰۰ سرباز شرکت کردند و جراحاتی برداشتند. آمار جراحات به شرح زیراست:

۷۰ نفر دست راستشان را از دست دادند
۷۵ نفر دست چپشان را از دست دادند
۸۰ نفر پای راست
۸۵ نفر پای چپ از دست دادند.

حد اقل تعداد افرادی که هر ۴ عضوشان را از دست دادن چندتاست؟ 

 ۲-  ۳-

حدس گلدباخ :

حدس گلدباخ در ریاضیات یکی از قدیمی‌ترین مسائل حل نشده نظریه اعداد است. این حدس می‌گوید:
هر عدد زوج بزرگ‌تر از ۲ را می‌توان به صورت حاصل‌جمع دو عدد اول نوشت.

مثال: ۲۰=۱۷+۳ یا ۱۰=۷+۳ و ۴=۲+۲ و ۱۲=۷+۵.

این مسئله در حدود ۲۶۰ سال پیش توسط یک پزشک آلمانی علاقه مند به اثبات قضیه‌های ریاضی مطرح شد.

یه سوال هوش قدیمی رو مطرح می کنم .

12 عدد سکه یکسان و یک اندازه که تنها یکی از آنها سبکتر یا سنگین تر از بقیه هست . چگونه می توان با 3 مرتبه وزن کردن سکه ها تعیین کرد که کدام سکه سبکتر یا سنگین تر بوده است ؟!؟!
( توجه :‌ نمی دانیم که سکه متفاوت سنگین تر از بقیه سکه ها هست یا سبکتر )  

بازی و ریاضی :

بازی و ریاضی :

ساخت پنج ضلعی منتظم با گره زدن کاغذ

 نوار بلند کاغذی آماده کنید که عرض یکسان داشته باشد.

برای ساخت یک پنج ضلعی منتظم با این نوار به تر تیب زیر عمل کنید:

1. دو سر نوار را بگیرید و با آن یک گره ساده بزنید

مانند شکل زیر:

2. گره را به آرامی سفت کنید و رد های کاغذ را صاف کنید.

3. نوار های اضافی را ببرید ،پنج ضلعی منتظم بوجود می آید.

4. گره را باز کنید و ذوزنقه های تشکیل شده را با هم بررسی و مقایسه کنید.

بازی و ریاضی :

بازی و ریاضی :

ساخت هفت ضلعی منتظم با گره زدن کاغذ :

نوار بلند کاغذی آماده کنید که عرض یکسان داشته باشد.

برای ساخت یک هفت ضلعی منتظم با این نوار به ترتیب زیر عمل کنید:

1. دو سر نوار را بگیرید و با آن یک گره ساده بزنید. (مانند پنج ضلعی منتظم)

2. گره را سفت نکنید و وسط گره (ناحیه ی 1) را در نظر داشته باشید.

3. مجددأ یک سر نوار را به قصد زدن گره دوم زیر سر دیگر برده ،و از ناحیه 1 (وسط گره اول) عبور دهید.

4. گره را به آرامی سفت کنید و رد های کاغذ را صاف کنید.

5. نوار های اضافی را ببرید ،هفت ضلعی منتظم بوجود می آید. 

زوش زسم نیمساز

روش رسم نیمساز  

 

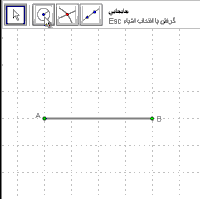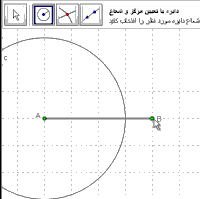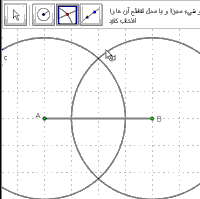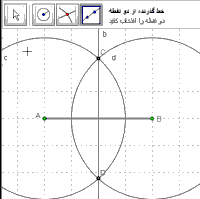
 برای رسم نیمساز روش های مختلفی وجوذ دارد اگر شما با روش متفاوتی می توانید نیمساز یک زاویه را رسم کنید لطفا در قسمت نظرات بنویسید .